Tian yuan shu, a method of algebraic computation using counting rods to solve problems, translates as "method of the heavenly element." The "heavenly element" refers to the unknown variable, which is usually represented by the letter x in modern algebra. As a positional system it makes use of the rod numerals to express polynomial (two or more algebraic terms) equations.

For example, 2x2 + 18x − 316 = 0 is represented as in Figure 1, and in Arabic numerals in Figure 2.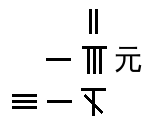                          

The 元 (yuan) represents the variable x, meaning the numbers in that line equate to 18x. The row underneath indicates the constant term (-316), while the row above represents the coefficient for the quadratic (x2) term. This framework can include arbitrarily high powers of the variable by adding more lines above, and negative powers by adding more lines below the constant term. Decimal values can also be expressed.

The theoretical origins of Tian yuan shu can be traced back to the mathematical treatise Jigu Suanjing by the early Tang Dynasty mathematician Wang Xiaotong. This book, completed around 626 AD, is the only mathematical classic among the Ten Mathematical Classics independently written by a Tang Dynasty scholar. In one volume, it contains 20 mathematical problems, covering astronomical calculations, calculations of solid volumes in civil engineering and hydraulic projects, and methods for solving cubic equations.

The Jigu Suanjing was the first text to systematically propose the "method of extracting roots with auxiliary terms (a numerical method for solving cubic equations with positive coefficients)." This method was later used by Jia Xian of the Northern Song Dynasty in his Diagram of the Origin of Root Extraction Methods for solving higher-order equations.

In modern times, Tian yuan shu's historical and cultural significance has become more evident. Academically, it is one of the world's earliest examples of symbolic algebra, predating the work of European mathematicians, such as Francois Viete, by more than 300 years.

Furthermore, its algorithmic thinking exemplifies the highly procedural and mechanized nature of ancient Chinese mathematics. Its attempts at symbolization demonstrate that across different civilizations, humanity has been exploring the use of abstract algebraic methods involving the replacement of specific numbers with symbols. In mathematics education, Tian yuan shu is often used to demonstrate the various ways in which equations can be developed, and to help students understand symbolic language.